“What is a retrospective pretest posttest?” You are not alone in wondering. I belong to the American Evaluation Association and subscribe to the EVALTALK listserv where members routinely enquire about this method. A retrospective pretest posttest is a type of survey instrument designed to reduce response shift bias.
If training participants, for example, are asked to rate their knowledge, skills, and abilities (KSAs) before and after receiving instruction, then they will often report lower KSAs after the training program. This is known as response shift bias and occurs because training participants tend to overestimate their KSAs beforehand. They become more knowledgeable during the training program and better equipped to gauge their own KSAs. Asking participants about their KSAs retrospectively, after the program, presumably reduces bias.
A retrospective pretest posttest is a single survey instrument administered after a program. It contain questions that asks respondents to rate their KSAs in hindsight as well as at the conclusion of the program. Survey questions are nearly identical and evenly spit between “Thinking back before the program…” and “Now, after the program.” I should note that in addition to reducing bias, a retrospective pretest posttest, administered once to a cohort, saves resources that would otherwise be spent on administering two or more surveys.
Here’s a good explanation posted to EVALTALK by Susan McNamara:
“[T]here are some cases where an after-the-fact measure really works out best. For example, in parent training (especially when court-ordered), the parents come to the first meeting thinking they know everything and that they’re perfect parents. If you give them a pretest now, they’re going to score themselves very highly. After three months or more of training, they’ve come to realize that no one is perfect, that there might be better ways of doing things, and perhaps the ways (e.g., of discipline) they were using before weren’t the best. Now, they might score themselves lower. If you give them a post-test, it looks like your program isn’t working, because their scores are going DOWN. However, if you use a retrospective pre-test (“fill this out now, but think about the attitudes and skills you had before you entered the program”) and a regular post-test, you are more likely to get a realistic change.”
I would like to research this method further because the scholarly literature has not fully addressed some questions. To what degree are retrospective self-ratings biased? Is there an optimal time to administer a “pretest” in a lagged fashion as to reduce bias (i.e., when does a self-rating shift to becoming unbiased)? Is there an item format that promotes unbiased responses when asked retrospectively (e.g., matrix vs. sequential vs. sectioned)? Should evaluators measure gain scores by supplementing or substituting self-ratings with test items? One could shed light on these questions by simultaneously administering a test measuring KSAs and a survey asking respondents to rate their KSAs throughout a training program or course.
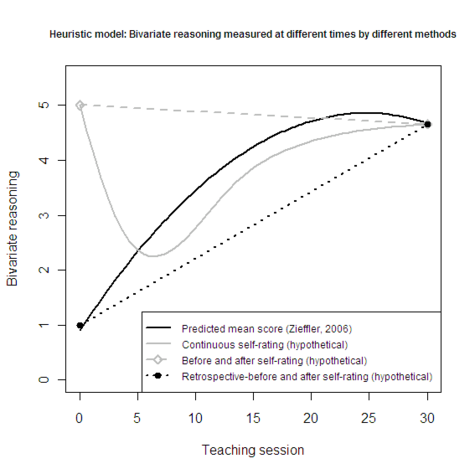
I created the heuristic model below to illustrate how tests and self-ratings might differ over time. The model uses the prediction equation from Dr. Andrew Zieffler’s dissertation as a starting point. He measured continuous longitudinal growth of bivariate reasoning ability among students in an educational psychology statistics class. The quadratic growth curve represents actual ability, while the other lines (gray and dotted) represent hypothetical self-rating scenarios that could be measured in a future study of response shift bias.
If one replicated Dr. Zieffler’s study with both test items and self-ratings, then the results could help evaluators and statistical educators choose an optimal data collection strategy that minimizes bias and cost. It would provide information for choosing knowledgeably between self-ratings and items that measure one’s knowledge, as well as between temporal options (i.e., traditional pre/post, lagged pre/post, retrospective pre/post). Topically, self-ratings of statistical reasoning may help with instructional planning and creating reliable and valid formative assessments with fewer items.
Click on thumbnail to see larger version:
R script
curve(.89856+.32046*x-.0064827*x^2, 0, 30, xlim=c(0,30), ylim=c(0,5.5),
lwd=2, xlab="Teaching session", ylab="Bivariate reasoning")
x=c(0,3,13,18,30)
y=c(5,3,3.5,4.2,4.65)
continuous=cbind(x,y)
lines(spline(continuous, n=50, method="natural"), lwd=2, col=8)
prepost=cbind(c(0,30), c(5,4.65))
points(prepost, pch=5, lty=2, lwd=2, col=8)
lines(prepost, lty=2, lwd=2, col=8)
retro=cbind(c(0,30), c(1,4.65))
points(retro, pch=16, lwd=2)
lines(retro, lwd=2, lty=3)
oldpar=par(no.readonly=T)
par(ps=9, cex.main=1)
legend("bottomright", c("Predicted mean score (Zieffler, 2006)",
"Continuous self-rating (hypothetical)",
"Before and after self-rating (hypothetical)",
"Retrospective-before and after self-rating (hypothetical) ")
,pch=c(NA,NA,5,16), col=c(1,8,8,1), lty=c(1,1,2,3), lwd=c(2,2,2,2), merge=T)
title(main="Heuristic model:
Bivariate reasoning measured at different times by different methods")
par(oldpar)