I was recently tasked with estimating the reliability of scores composed of items on different scales. The lack of a common scale could be seen in widely varying item score means and variances. As discussed by Graham, it’s not widely known in applied educational research that Cronbach’s alpha assumes essential tau-equivalence and underestimates reliability when the assumption isn’t met. A friend made a good suggestion to consider stratified alpha, which is commonly used to estimate internal consistency when scores are composed of multiple choice items (scored 0-1) and constructed response items (e.g., scored 0-4). However, the assessment with which I was concerned does not have clear item-type strata. I decided to estimate congeneric reliability because it makes few assumptions (e.g., unidimensionality) and doesn’t require grouping items into essentially tau-equivalent strata.
With the help of Graham’s paper and a LISREL tutorial by Raykov I wrote an  program that estimates congeneric reliability. The program uses Fox’s sem() library to conduct the confirmatory factor analysis with minimal constraints (variance of common true score fixed at 1 for identifiability). The estimated loadings and error variances are then summed to calculate reliability (i.e., the ratio of true score variance to observed score variance) as:
program that estimates congeneric reliability. The program uses Fox’s sem() library to conduct the confirmatory factor analysis with minimal constraints (variance of common true score fixed at 1 for identifiability). The estimated loadings and error variances are then summed to calculate reliability (i.e., the ratio of true score variance to observed score variance) as:
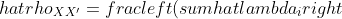 ^ 2} {left( sum hat{lambda}_i right) ^ 2 + sum hat{delta}_{i} }) .
.
I obtained a congeneric reliability estimate of 0.80 and an internal consistency estimate of 0.58 for the scores I was analyzing. If the items had been essentially tau-equivalent, then the reliability estimates would have been the same. If I had assumed tau-equivalence, than I would have underestimated the reliability of the total scores (and overestimated standard errors of measurement). The example below replicates Graham’s heuristic example.
> ############################################
> #Replicate results from Graham (2006) to check congeneric reliability code/calculations.
>
> library(sem)
> library(psych)
> library(stringr)
>
> #Variance/covariance matrix
> S.graham <- readMoments(diag = T, names = paste("x", 1:7, sep = ""))
1: 4.98
2: 4.60 5.59
4: 4.45 4.42 6.30
7: 3.84 3.81 3.66 6.44
11: 5.71 5.67 5.52 4.91 11.86
16: 23.85 23.68 22.92 19.87 34.28 127.65
22: 46.53 46.20 44.67 38.57 62.30 244.36 471.95
29:
Read 28 items
>
> ############################################
> #A function to estimate and compare congeneric reliability and internal consistency
> funk.congeneric <- function(cfa.out) {
+ names.loadings <- str_detect(names(cfa.out$coeff), "loading")
+ names.errors <- str_detect(names(cfa.out$coeff), "error")
+ r.congeneric <- sum(cfa.out$coeff[names.loadings]) ^ 2 /
+ (sum(cfa.out$coeff[names.loadings]) ^ 2 + sum(cfa.out$coeff[names.errors]))
+ round(c("Congeneric" = r.congeneric, "Alpha" = alpha(cfa.out$S)$total$raw_alpha), 2)
+ }
>
> ############################################
> #Congeneric model; tau-equivalent items
> model.graham <- specifyModel()
1: T -> x1, loading1
2: T -> x2, loading2
3: T -> x3, loading3
4: T -> x4, loading4
5: T -> x5, loading5
6: x1 <-> x1, error1
7: x2 <-> x2, error2
8: x3 <-> x3, error3
9: x4 <-> x4, error4
10: x5 <-> x5, error5
11: T <-> T, NA, 1
12:
Read 11 records
> cfa.out <- sem(model = model.graham, S = S.graham, N = 60)
> summary(cfa.out)
Model Chisquare = 0.11781 Df = 5 Pr(>Chisq) = 0.99976
Chisquare (null model) = 232.13 Df = 10
Goodness-of-fit index = 0.9992
Adjusted goodness-of-fit index = 0.99761
RMSEA index = 0 90% CI: (NA, NA)
Bentler-Bonnett NFI = 0.99949
Tucker-Lewis NNFI = 1.044
Bentler CFI = 1
SRMR = 0.0049092
AIC = 20.118
AICc = 4.6076
BIC = 41.061
CAIC = -25.354
Normalized Residuals
Min. 1st Qu. Median Mean 3rd Qu. Max.
-0.038700 -0.008860 -0.000002 0.004700 0.002450 0.119000
R-square for Endogenous Variables
x1 x2 x3 x4 x5
0.9286 0.8175 0.6790 0.4962 0.5968
Parameter Estimates
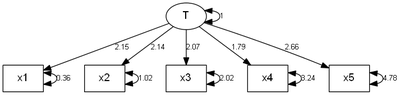
Estimate Std Error z value Pr(>|z|)
loading1 2.15045 0.21595 9.9580 2.3263e-23 x1 <--- T
loading2 2.13776 0.24000 8.9073 5.2277e-19 x2 <--- T
loading3 2.06828 0.26941 7.6770 1.6281e-14 x3 <--- T
loading4 1.78754 0.29136 6.1352 8.5040e-10 x4 <--- T
loading5 2.66040 0.38141 6.9752 3.0535e-12 x5 <--- T
error1 0.35559 0.17469 2.0356 4.1793e-02 x1 <--> x1
error2 1.02000 0.25339 4.0255 5.6861e-05 x2 <--> x2
error3 2.02222 0.41688 4.8509 1.2293e-06 x3 <--> x3
error4 3.24471 0.62679 5.1767 2.2583e-07 x4 <--> x4
error5 4.78227 0.94911 5.0387 4.6871e-07 x5 <--> x5
Iterations = 21
> pathDiagram(cfa.out, edge.labels = "values", ignore.double = F, rank.direction = "TB")
> funk.congeneric(cfa.out)
Congeneric Alpha
0.91 0.91
>
> ############################################
> #Congeneric model; tau-inequivalent items
> model.graham <- specifyModel()
1: T -> x1, loading1
2: T -> x2, loading2
3: T -> x3, loading3
4: T -> x4, loading4
5: T -> x7, loading7
6: x1 <-> x1, error1
7: x2 <-> x2, error2
8: x3 <-> x3, error3
9: x4 <-> x4, error4
10: x7 <-> x7, error7
11: T <-> T, NA, 1
12:
Read 11 records
> cfa.out <- sem(model = model.graham, S = S.graham, N = 60)
> summary(cfa.out)
Model Chisquare = 0.0072298 Df = 5 Pr(>Chisq) = 1
Chisquare (null model) = 353.42 Df = 10
Goodness-of-fit index = 0.99995
Adjusted goodness-of-fit index = 0.99985
RMSEA index = 0 90% CI: (NA, NA)
Bentler-Bonnett NFI = 0.99998
Tucker-Lewis NNFI = 1.0291
Bentler CFI = 1
SRMR = 0.0010915
AIC = 20.007
AICc = 4.497
BIC = 40.951
CAIC = -25.464
Normalized Residuals
Min. 1st Qu. Median Mean 3rd Qu. Max.
-2.76e-02 -1.27e-04 -1.00e-07 -1.92e-03 1.96e-04 3.70e-03
R-square for Endogenous Variables
x1 x2 x3 x4 x7
0.9303 0.8171 0.6778 0.4942 0.9902
Parameter Estimates
Estimate Std Error z value Pr(>|z|)
loading1 2.15247 0.212984 10.10624 5.1835e-24 x1 <--- T
loading2 2.13719 0.237279 9.00711 2.1156e-19 x2 <--- T
loading3 2.06646 0.266419 7.75646 8.7336e-15 x3 <--- T
loading4 1.78392 0.287599 6.20279 5.5470e-10 x4 <--- T
loading7 21.61720 2.015041 10.72792 7.5272e-27 x7 <--- T
error1 0.34688 0.090227 3.84451 1.2080e-04 x1 <--> x1
error2 1.02240 0.200635 5.09584 3.4720e-07 x2 <--> x2
error3 2.02973 0.382466 5.30694 1.1148e-07 x3 <--> x3
error4 3.25764 0.605376 5.38118 7.3998e-08 x4 <--> x4
error7 4.64661 6.387765 0.72742 4.6697e-01 x7 <--> x7
Iterations = 38
> pathDiagram(cfa.out, edge.labels = "values", ignore.double = F, rank.direction = "TB")
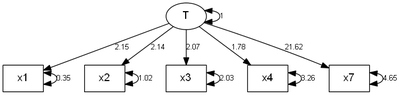
> funk.congeneric(cfa.out)
Congeneric Alpha
0.99 0.56
![]() because it helps me learn methods far better than simply reading about them or using a pre-existing software package. In that vein, I decided to write some functions to conduct G and D studies with
because it helps me learn methods far better than simply reading about them or using a pre-existing software package. In that vein, I decided to write some functions to conduct G and D studies with ![]() . I’ve been using synthetic data from Brennan’s book and Shavelson and Webb’s book to ensure that my results match theirs. The nice thing about using
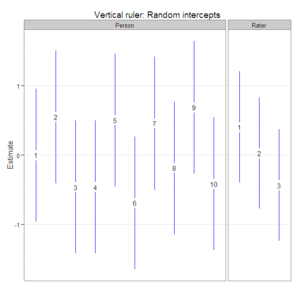
. I’ve been using synthetic data from Brennan’s book and Shavelson and Webb’s book to ensure that my results match theirs. The nice thing about using ![]() for G theory is that you can choose functions for many different packages to fully apply G theory. For example, by using lme4 to estimate variance components, arm to extract standard errors of random intercepts, and ggplot2 to create faceted plots, I am able to create “vertical ruler” plots, which are prevalent among practitioners of many-facets Rasch. Such plots make it easy to identify the (statistically significantly) highest and lowest performers as well as the most lenient and stringent raters.
for G theory is that you can choose functions for many different packages to fully apply G theory. For example, by using lme4 to estimate variance components, arm to extract standard errors of random intercepts, and ggplot2 to create faceted plots, I am able to create “vertical ruler” plots, which are prevalent among practitioners of many-facets Rasch. Such plots make it easy to identify the (statistically significantly) highest and lowest performers as well as the most lenient and stringent raters.
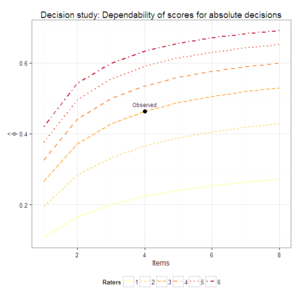
![]() . The plots were produced from Brennan’s synthetic data set number 4, and the dependability coefficients match those from GENOVA. I’ve never developed an
. The plots were produced from Brennan’s synthetic data set number 4, and the dependability coefficients match those from GENOVA. I’ve never developed an ![]() package, but given that no one else has so far, I’d be interested in doing so with the code I’m developing.
package, but given that no one else has so far, I’d be interested in doing so with the code I’m developing.