EvaluationDashboard.com

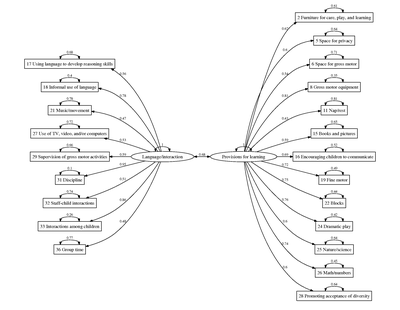
The Early Childhood Environment Rating Scale (Revised; ECERS-R) was designed to measure process quality in child care centers, but the data set that I have been analyzing contains ratings of center classrooms and family child care (FCC) homes. A sizable portion of the program’s budget was spent on training ECERS-R raters. Training them to reliably use both the ECERS-R and the Family Day Care Rating Scale (FDCRS) was cost prohibitive.

Was it unfair to rate FCC homes with the ECERS-R instrument? I conducted a differential item functioning (DIF) analysis to answer that question and remedy any apparent biases. Borrowing a quasi-experimental matching technique (not for the purpose of inferring causality), I employed propensity score weighting to match center classrooms with FCC homes of similar quality. For each item j, classroom/home i‘s propensity score (i.e., predicted probability of being an FCC home) was estimated using the following logistic regression model:

where FCC is a focal group dummy variable (1 if home; 0 if center) and Total_c stands for corrected total score (i.e., mean of item scores excluding item j). Classroom weights were calculated from the inverse of a site’s predicted probability of its actual type and normalized so the weights sum to the original sample size:

Such weights can induce overlapping distributions (i.e., balanced groups). In this case, the weights were were applied via weighted least squares (WLS) regression of item scores on corrected total scores and the focal group dummy, as well as an interaction term to consider the possibility of nonuniform/crossing DIF:

By minimizing , WLS gave classrooms/homes with weights greater than 1 more influence over parameter estimates and decreased the influence of those with weights less than 1.

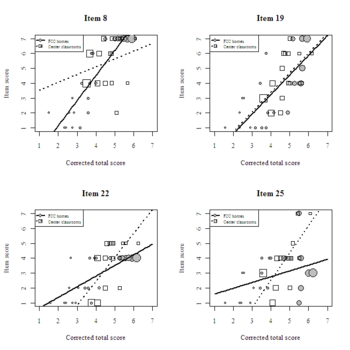
The results suggest that three provisions for learning items function differentially and in a non-uniform manner, as indicated by statistically significant interactions (see the table below). None of the language/interaction items exhibited DIF. The regression coefficients suggest that differentially functioning ECERS items did not consistently favor one type of care over the other. After dropping the three differentially functioning items from the provisions for learning scale and re-running the DIF analysis, none of the remaining items exhibited differential functioning.

Summary of WLS estimates: Differentially functioning ECERS items

Plot of weighted observations and fitted lines: Three crossing DIF items and one fair item (Item 19: Fine motor activities)

Scores from the final provisions for learning scale exhibited good reliability of α = 0.87. Scores from the language/interaction scale also exhibited good reliability of α = 0.86. None of the items detracted problematically from overall reliability (i.e., the most that α increased after dropping any item was 0.01 in one instance).

I want to caution readers against generalizing the factor structure and DIF findings beyond this study because the sample is small in size (n = 38 classrooms/homes) and was drawn from a specific population (urban child care businesses subject to local market conditions and state-specific regulations). I largely avoided making statistical inferences in the preceding analyses by exploring the data and comparing relative fit, but in this case I used a significance level of 0.05 to infer DIF. The data do not provide a large amount of statistical power, so there could be more items that truly function differentially. For the final paper, I may apply a standardized effect size criterion. Standardized effect sizes are used to identify DIF with very large samples because the p-values would lead one to infer DIF for almost every item. De-emphasizing p-values in favor of effect sizes may be appropriate with small samples, too.

I followed up the exploratory factor analysis (EFA) of the Early Childhood Environment Rating Scale (ECERS-R) with a confirmatory model comparison of the six-, two-, and one-factor solutions. The six-factor specification adhered to the original subscales in the ECERS-R instrument (after dropping highly skewed items); the two-factor specification simply restricted the minor loadings from the EFA to zero; and the one-factor specification restricted items to zero if they loaded less than |0.3| in the one-factor EFA solution.

The six-factor model did not converge, and the two-factor model exhibited better fit than the one-factor model. These results support earlier findings by Sakai and colleagues (2003) and Cassidy and colleagues (2005) that the ECERS-R measures two latent factors: provisions for learning and language/interaction experienced by children.

The goal of this analysis was to find a factorially simple solution. Higher order or hierarchical models of greater complexity would be worth considering in light of evolving theories and needs surrounding measures of child care quality and given that:

• several ECERS-R items cross-loaded in the EFAs and were subsequently excluded
• the overall fit of the two-factor model was poor
• the estimated correlation between the latent factors was somewhat large (0.68).

Comparison of one- and two-factor models

Measurement model (click image)

The Early Childhood Environment Rating Scale, revised edition (ECERS-R; Harms, Clifford, & Cryer, 1998), is an instrument used widely to observe and rate levels of process quality in child care centers. The authors have divided the instrument into six subscales to help ensure broad and flexible coverage of various aspects of child care quality. (The ECERS-R actually contains seven subscales, but the last one pertains to parents and staff instead of process quality experienced by children.) Psychometric analyses suggest the ECERS-R actually measures two latent dimensions of quality at most. Perlman, Zellman, and Le (2004) concluded that process quality, as measured by the ECERS-R, is unidimensional. Sakai and colleagues (2003) and Cassidy and colleagues (2005) concluded that the ECERS-R measures two latent dimensions, although their factor loadings and interpretations differ across the two studies.

I am writing a paper to present at the upcoming American Educational Research Association (AERA) conference in Denver. The paper will report results from a structural equation mediation model of the influence of on-site child care professional development on school readiness through child care quality. Given the lack of agreement among the earlier psychometric analyses of the ECERS-R, I conducted an exploratory factor analysis to see if I could replicate findings from one of the earlier studies. As shown in the table below, my preliminary results and interpretations do not align perfectly with either of the two-factor solutions from the earlier studies, but the similarities helped me decide which items to drop and which of my interpretations to keep. I plan to use a confirmatory factor analysis to formally compare model fit between the one- and two-factor solution before estimating the mediation model. I hope the summary below will help others who are wrestling with the possibility of multiple dimensions of child care quality as measured by the ECERS-R.

Summary of ECERS-R two-factor solutions from three studies

Note: Empty cells indicate loadings less than |0.3|, cross-loadings greater than |0.3|, or items skewed greater than |2|. Item 37, which asks about provisions for children with disabilities was excluded due to high missingness.

My last post described how test development designs could be thought of as multistage sampling designs and how multilevel Rasch could be used to estimate parameters under that assumption. I decided to use to compare estimates from the usual Rasch model, the generalized linear model (GLM) with a logit link, and generalized linear mixed-effects regression (GLMER), treating items as fixed then random effects. The GLMER model with item fixed effects exhibited the best fit of the Law School Admission Test (LSAT) data provided with the ltm package. Moreover, intraclass correlation has reduced the effective sample size relative to simple random sampling, lending further support to the multilevel Rasch approach.

#Load libraries.
library(ltm)
library(lme4)
library(xtable)

#Prepare data for GLM.
LSAT.long <- reshape(LSAT, times=1:5, timevar="Item", varying=list(1:5), direction="long")
names(LSAT.long) <- c("Item", "Score", "ID")
LSAT.long$Item <- as.factor(LSAT.long$Item)
LSAT.long$ID <- as.factor(LSAT.long$ID) #Compute Rasch, GLM, and GLMER estimates and compare fit.
out.rasch <- rasch(LSAT, constraint=cbind(ncol(LSAT)+1, 1))
print(xtable(summary(out.rasch)$coefficients, digits=3), type="html")

out.glm <- glm(Score ~ Item, LSAT.long, family="binomial")
print(xtable(summary(out.glm)$coefficients, digits=3), type="html")

out.glmer <- glmer(Score ~ Item + (1|ID), LSAT.long, family="binomial")
print(xtable(summary(out.glmer)@coefs, digits=3, caption="Fixed effects"), type="html", caption.placement="top")
print(xtable(summary(out.glmer)@REmat, digits=3, caption="Random effects"), type="html", caption.placement="top", include.rownames=F)

out.glmer.re <- glmer(Score ~ (1|Item) + (1|ID), LSAT.long, family="binomial")
print(xtable(summary(out.glmer.re)@coefs, digits=3, caption="Fixed effects"), type="html", caption.placement="top")
print(xtable(summary(out.glmer.re)@REmat[,-6], digits=3, caption="Random effects"), type="html", caption.placement="top", include.rownames=F)

print(xtable(AICs.Rasch.GLM <- data.frame(Rasch=summary(out.rasch)$AIC, GLM=summary(out.glm)$aic, GLMER.fe=summary(out.glmer)@AICtab$AIC, GLMER.re=summary(out.glmer.re)@AICtab$AIC, row.names="AIC"), caption="Akaike's information criteria (AICs)"), type="html", caption.placement="top")

#Easiness estimates.
easiness <- data.frame(Rasch=out.rasch$coefficients[,1],
GLM=c(out.glm$coefficients[1], out.glm$coefficients[1]+out.glm$coefficients[-1]),
GLMER.fe=c(fixef(out.glmer)[1], fixef(out.glmer)[1]+fixef(out.glmer)[-1]),
GLMER.re=fixef(out.glmer.re)+unlist(ranef(out.glmer.re)$Item))
print(xtable(easiness, digits=3), type="html")

#Estimated probabilities of a correct response.
pr.correct <- sapply(easiness, plogis)
row.names(pr.correct) <- row.names(easiness)
print(xtable(pr.correct, digits=3), type="html")

#Difficulty estimates.
difficulties <- easiness*-1
print(xtable(difficulties, digits=3), type="html")

#Calculate design effects and effective samples sizes from intraclass correlation coefficients and sampling unit sizes.
multistage.consequences <- function(ICC, N) {
M <- nrow(LSAT.long)
n <- M/N #number of responses per item
deff <- 1+(n-1)*ICC
M.effective <- trunc(M/deff)
return(data.frame(ICC, M, N, n, deff, M.effective))
}
model.ICC.Item <- glmer(Score ~ 1 + (1|Item), family=binomial, data=LSAT.long)
ICC.Item <- as.numeric(VarCorr(model.ICC.Item)$Item)/(as.numeric(VarCorr(model.ICC.Item)$Item)+pi^2/3)
multistage.Item <- multistage.consequences(ICC.Item, 5)
model.ICC.ID <- glmer(Score ~ 1 + (1|ID), family=binomial, data=LSAT.long)
ICC.ID <- as.numeric(VarCorr(model.ICC.ID)$ID)/(as.numeric(VarCorr(model.ICC.ID)$ID)+pi^2/3)
multistage.ID <- multistage.consequences(ICC.ID, 1000)
multistage <- data.frame(cbind(t(multistage.Item), t(multistage.ID)))
names(multistage) <- c("Item", "ID")
print(xtable(multistage, digits=3), type="html")

#Plot test characteristic curves
plot.tcc <- function(difficulties, add, col, lty) {
thetas <- seq(-3.8,3.8,length=100)
temp <- matrix(nrow=length(difficulties), ncol=length(thetas))
for(i in 1:length(thetas)) {for(theta in thetas) temp[,which(thetas==theta)] <- plogis(theta-difficulties)}
if(missing(add)) {plot(thetas, colSums(temp), ylim=c(0,5), col=NULL, ylab=expression(tau), xlab=expression(theta), main="Test characteristic curves")}
lines(thetas, colSums(temp), col=col, lty=lty)
}
plot.tcc(difficulties=difficulties[,1], col="black", lty=1)
plot.tcc(difficulties=difficulties[,2], add=T, col="blue", lty=2)
plot.tcc(difficulties=difficulties[,3], add=T, col="red", lty=3)
plot.tcc(difficulties=difficulties[,4], add=T, col="green", lty=4)
legend("bottomright", c("Rasch", "GLM", "GLMER, fixed items", "GLMER, random items "), col=c("black", "blue", "red", "green"), lty=1:4)